|
Моментът на
сила е количествена мярка за въртеливото действие на силата, приложена
върху дадено тяло.
Момент на сила спрямо точка - Моментът на
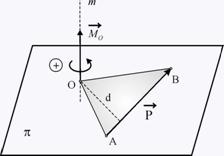
силата 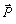 спрямо точката O (моментов център) е векторът спрямо точката O (моментов център) е векторът 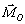 (фиг. 1),
определен със следните елементи: 1) приложна точка - т. О; 2) директриса
(правата Om)-
перпендикулярна на равнината p, определена от т.О и силата (фиг. 1),
определен със следните елементи: 1) приложна точка - т. О; 2) директриса
(правата Om)-
перпендикулярна на равнината p, определена от т.О и силата 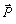 ; 3) големина ; 3) големина 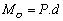 [N.m], където перпендику-лярното разстояние d от
моментовия център до директрисата на силата се нарича рамо на силата; 4) посока - определена от правилото на
дясната ръка: ако се поставят пръстите на дясната ръка по посока на
силата така, че точката - моментов център да остава откъм дланта, то
тогава палецът показва посоката на момента. [N.m], където перпендику-лярното разстояние d от
моментовия център до директрисата на силата се нарича рамо на силата; 4) посока - определена от правилото на
дясната ръка: ако се поставят пръстите на дясната ръка по посока на
силата така, че точката - моментов център да остава откъм дланта, то
тогава палецът показва посоката на момента.
фиг. 1 фиг. 2
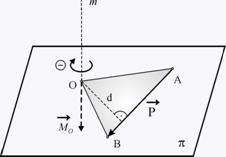
Ако посоката на момента е “нагоре”
от равнината p (фиг. 1), се приема той да се
счита за положителен, а ако е насочен “надолу” (фиг. 2) - за отрицателен.
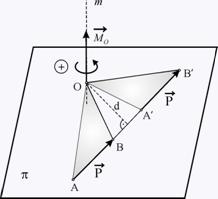
При разглеждане на сили в чертожната равнина, моментовият вектор 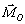 не може да се
изобрази. Тогава се ползва следното
условно представяне с
насочени дъги: не може да се
изобрази. Тогава се ползва следното
условно представяне с
насочени дъги:  - при положителен момент (въртене в
посока, обратна на часовниковата стрелка) и съответно - при положителен момент (въртене в
посока, обратна на часовниковата стрелка) и съответно  - при отрицателен (въртене в посока на
часовниковата стрелка). - при отрицателен (въртене в посока на
часовниковата стрелка).
◊ Моментът
на сила спрямо точка е типичен пример за “свързан” (фиксиран към точка) вектор и се характеризира със следните основни свойства:
- Моментът не се променя при плъзгане на силата по
нейната директриса - фиг. 3. (Защото в механиката силата е “плъзгащ" вектор).
 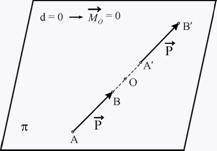
фиг. 3 фиг. 4
- Моментът е равен на нула в два случая: когато
големината на силата е равна на нула или когато директрисата на силата пресича
точката, спрямо която се дефинира
(защото рамото на силата е равно
на нула) - фиг. 4.
- Моментът променя посоката си, ако се промени посоката на
силата - фиг.1 и фиг.2.
|