|
Ротационно
движение (ротация) на твърдо тяло - когато
две
точки от тялото (или неизменно свързани с него) остават неподвижни по
време на движението (фиг. 1). Двете точки определят една права, която се
нарича ос на ротация (ос на въртене).
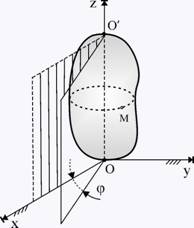 фиг. 1 фиг. 1
◊ Закон на движение - Положението на тялото във всеки момент от
време се определя от:
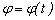 , [rad], , [rad],
където 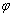 е ъгълът между
неподвижната и подвижната равнини, минаващи през ротационната ос (фиг.
1). е ъгълът между
неподвижната и подвижната равнини, минаващи през ротационната ос (фиг.
1).
◊ Скорост - Тялото има ъглова скорост, представляваща
първа производна спрямо времето на ъгъла на въртене:
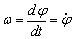 , [rad/s] или [s-1]. , [rad/s] или [s-1].
Знакът на w може да бъде + или – в зависимост от посоката
на въртене на тялото. Когато то се върти в посока, обратна на въртенето
на часовниковата стрелка, ъгловата скорост w е положителна, а при въртене по посока на часовниковата стрелка
- w е
отрицателна.
◊ Ускорение - Ъгловото ускорение на тялото се дефинира като първа
производна спрямо времето на ъгловата скорост или респективно втора
производна на ъгъла на завъртане на тялото
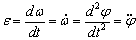 , [rad/s2] или [s-2]. , [rad/s2] или [s-2].
Ъгловото ускорение също може да
бъде с + или - знак. Когато посоката му съвпада с посоката на
часовниковата стрелка e е
отрицателено, в обратния случай - e е положително.
◊ Частни
случаи на ротационно движение на тяло
Ако големината на ъгловата скорост
с течение на времето нараства, въртенето на тялото е ускорително. В този случай w и e имат
еднакви знаци.
Ако
големината на ъгловата скорост с течение на времето намалява, ротацията е
закъснителна.
Тогава w и e са с противоположни знаци.
Тялото
извършва раномерно ротационно
движение, когато
e
=
0, а ъгловата
скорост w = const.
Ако e = const,
движението на ротиращото тяло се нарича равнопроменливо.
◊ Скорости и ускорения на точките от тялото
|
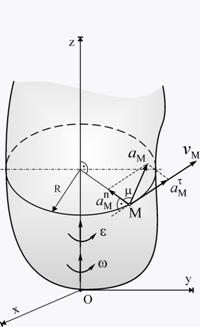 фиг. 2 фиг. 2
|
Всяка
произволна точка от тялото, нележаща на оста на ротация (фиг. 2),
описва окръжност в равнина, перпендикулярна на оста на ротация.
Въпросната окръжност представлява траекторията на точката.
|
Скоростта на такава точка (например т. М) е вектор,
насочен по допирателната към траекторията (окръжността), с посока
съвпадаща с посоката на въртене (на ъгловата скорост) и с големина,
определяна като
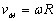 , [m/s], , [m/s],
където 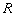 е разстоянието
от точката до оста на въртене. е разстоянието
от точката до оста на въртене.
Ускорението на такава точка
има две компоненти: - тангенциална (въртеливо ускорение) с направление,
съвпадащо с тангентата към траекторията и големина
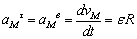 [m/s2] [m/s2]
и нормална (центростремително ускорение) с
направление перпендикулярно на оста на въртене, посока към нея и големина
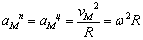 [m/s2]. [m/s2].
Големината на пълното ускорение е
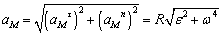 [m/s2], [m/s2],
а направлението и посоката му
се определят от векторната сума на 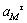 и и 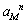 . Острият ъгъл (ъгъл m) между пълното и центростремително ускорения се определя чрез
отношението . Острият ъгъл (ъгъл m) между пълното и центростремително ускорения се определя чрез
отношението 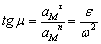 . .
|