|
Траекторията на една
точка (т. М) е съвкупността от последователните положения, които
подвижната точка заема по време на движението (фиг. 1).
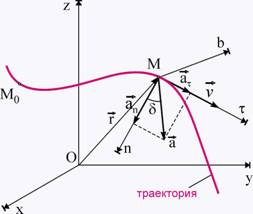 фиг. 1 фиг. 1
Уравненията на закона за
движение по координатния метод, т.е. x=x(t); y=y(t); z=z(t) са едновременно и параметрични уравнения на
траекторията. Като се задават последователни стойности на параметъра t, се получава кривата, която описва
точката при своето движение, т.е. нейната траектория. За да се получи декартовото уравнение на линията,
върху която лежи траекторията, трябва да се изключи параметъра t от нейните параметрични уравнения
(напр. за равнинния случай се определя зависимост от вида x=x(y) или y=y(x) ). Трябва да се има предвид, че
действителното геометрично място на точката може да не бъде върху цялата
линия, описана с уравненията x=x(y) или y=y(x). Причина за това е, че времето
е величина винаги ≥0, а функциите, заложени в параметричните
уравнения понякога са ограничени в определен интервал.
|